Tags and keywords
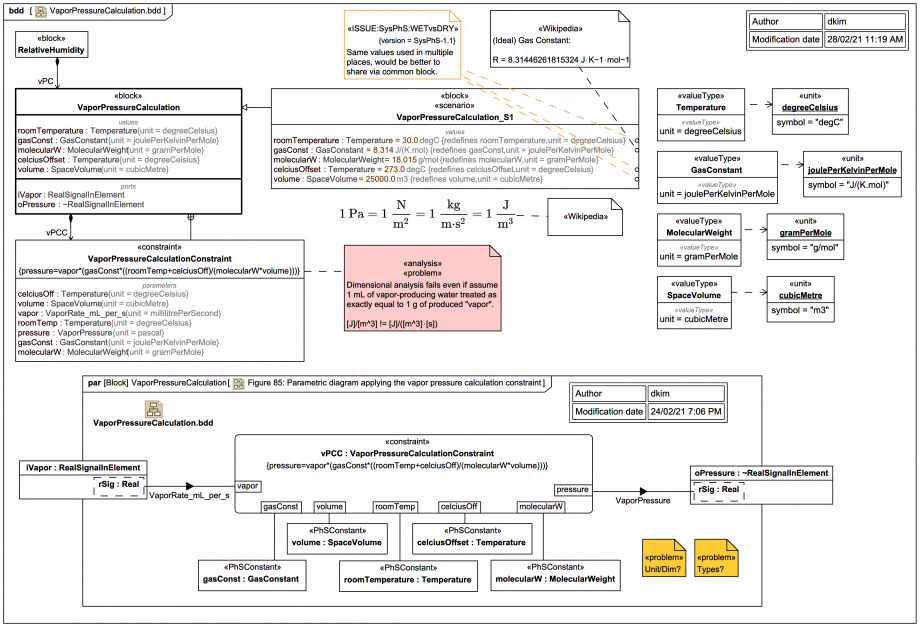
This diagram shows the Block
VaporPressureCalculation with a supporting ConstraintBlock VaporPressureCalculationConstraint:The Constraint equation is:
{pressure=vapor*(gasConst*((roomTemp+celciusOff)/(molecularW*volume)))}P⋅V = n⋅R⋅T ideal gas law, where n is the number of moles and R = 8.314 J/(K⋅mol) you get:
pressure*volume=(vapor/molecularW)*gasConst*(roomTemp+celciusOff)This implies vapor/molecularW is just equivalent to the number of moles n. But this makes no sense if "vapor" is elsewhere a rate mL/s, it only makes sense if "vapor" is a mass (in g).
Aha, maybe they've used a sneaky not-quite-accurate trick in the spec equation:
As it happens, 1 mL of water at most temperatures and pressures does not have a mass of exactly 1g. But even if the "vapor" were taken as g/s then the dimensional analysis suggests there is a major problem, you'd end up with the output being a pressure rate:
Also:
If you assume the
volume is litres (L) the dimensional analysis is off by a factor of 1000.
So it seems this assumption used in this trail is correct:
And we are indeed dealing with a commercial humidifier for a large building, not a "humidified room":
Notes
[MODELLING, NAVIGATION, PATTERN, TIP, TOOL]{STRONG} Webel: UML/SysML: Navigation: ALWAYS offer a way out of a diagram (usually up a hierarchy, but possibly across) using a navigable symbol (linked to a diagram) and/or a diagram symbol. Avoid "cul-de-sacs"! [But beware of shared package cross-dependencies]